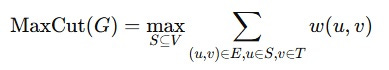Kvantové výpočty v nelineárnom čase

Jessica Rose, 13. januára 2025

Je to niečo, čo môžeme využiť?

Kvantové počítače fungujú tak, že na vykonávanie výpočtov využívajú princípy kvantovej mechaniky, konkrétne superpozície a previazanosti. Na rozdiel od klasických počítačov, ktoré používajú bity ako 0 alebo 1, kvantové počítače používajú kvantové bity alebo qubity, ktoré môžu existovať vo viacerých stavoch súčasne (superpozícia) – v podstate predstavujú 0 aj 1 súčasne. To umožňuje kvantovým počítačom spracovávať obrovské množstvo možností naraz.

Keď sú qubity previazané, stav jedného qubitu môže byť priamo korelovaný s iným bez ohľadu na vzdialenosť medzi nimi, čo umožňuje komplexné operácie, pri ktorých zmena jedného qubitu okamžite ovplyvní jeho previazaného partnera. Kvantové algoritmy využívajú tieto vlastnosti na riešenie určitých typov problémov, ako je optimalizácia, kryptografia alebo simulácia kvantových systémov, oveľa rýchlejšie ako klasické počítače tým, že skúmajú viacero výpočtových ciest súčasne.
Udržiavanie týchto kvantových stavov (koherencie) je však náročné kvôli interakciám prostredia, ktoré spôsobujú dekoherenciu, čo si vyžaduje sofistikované techniky opravy chýb.
Optimalizačné problémy zahŕňajú určitý stupeň pravdepodobnosti, čo podľa môjho chápania znamená, že sa riešia s ohľadom na lineárny čas.

Kvantové počítače využívajú princípy kvantovej mechaniky, kde sú kľúčové superpozícia, previazanie a kvantová interferencia. Ak uvažujeme o svete, kde je čas nelineárny, tieto kvantové javy by mohli interagovať s časom spôsobom, ktorý by mohol zásadne ovplyvniť kvantové počítače:

1. Superpozícia a čas:

   • Tradičná superpozícia: V lineárnom čase existujú kvantové bity (qubity) vo viacerých stavoch súčasne, kým sa nezmerajú. Ak je čas nelineárny, pojem „kým sa nezmeria“ môže byť menej jednoduchý. Namiesto kolapsu do jedného stavu v konkrétnom okamihu by superpozícia mohla predstavovať všetky stavy vo všetkých časoch súčasne, čo by potenciálne umožnilo výpočty, ktoré pokrývajú alebo využívajú viacero časových stavov naraz.

   • Časová superpozícia: V nelineárnom časovom rámci by qubit nemusel byť len v superpozícii stavov, ale mohol by byť aj v superpozícii rôznych časov alebo časových skúseností, čo by viedlo k výpočtom, pri ktorých čas operácie nie je pevne stanovený, ale je súčasťou kvantového stavu.

2. Entanglement*:

   • Časovo previazané stavy: Entanglement (kvantové prepojenie) by sa mohol rozšíriť na rôzne časové stavy, čo znamená, že qubity by mohli byť korelované nielen priestorovo, ale aj časovo. To by mohlo viesť k novým formám kvantovej komunikácie alebo výpočtov, kde sa informácie zdieľajú alebo počítajú v rôznych „časoch“ súčasne.

   • Spätné väzby: Ak kauzalita nie je striktne lineárna, entanglement by mohol umožniť spätné väzby vo výpočtoch, kde výstup výpočtu ovplyvňuje jeho vstup nelineárnym časovým spôsobom, čo by mohlo viesť k novým algoritmom alebo dokonca paradoxným výpočtovým scenárom.

3. Kvantová interferencia:

   • Interferencia naprieč časom: Cesty, ktorými sa kvantové častice uberajú pri výpočte, by mohli interferovať nielen v priestore, ale aj naprieč rôznymi časovými cestami. To by mohlo znamenať, že interferenčné vzory sa vyskytujú spôsobmi, ktoré sú menej predvídateľné alebo zložitejšie, čo potenciálne umožňuje výpočty, ktoré využívajú tento časový rozmer na zvýšenie výpočtového výkonu alebo účinnosti.

4. Korekcia chýb a dekoherencia:

   • Nelineárna korekcia chýb: V lineárnom časovom modeli sa kvantová korekcia chýb zameriava na zachovanie koherencie v čase. V nelineárnom čase sa chyby nemusia šíriť priamym spôsobom, čo môže zjednodušiť alebo skomplikovať opravu chýb v závislosti od toho, ako sa časové stavy navzájom ovplyvňujú.

   • Dekoherencia: Ak je čas nelineárny, môže sa zmeniť samotná koncepcia interakcie systémov s prostredím a straty kvantových vlastností, čo môže ponúknuť nové stratégie na udržanie kvantových stavov alebo naopak, urobiť z dekoherencie ešte zložitejší problém.

5. Algoritmické dôsledky:

   • Nové kvantové algoritmy: Algoritmy by mohli byť vyvinuté tak, aby špecificky využívali nelineárne časové vlastnosti, možno na riešenie problémov, ktoré si vyžadujú pochopenie alebo manipuláciu s časovými konfiguráciami, a nie len s priestorovými.

   • Simulácia nelineárnych systémov: Kvantové počítače by sa mohli stať ešte vhodnejšími na simuláciu systémov, v ktorých sa čas správa nelineárne, čo by umožnilo nahliadnuť do javov, ako sú čierne diery, červie diery alebo iné exotické fyzikálne javy, v ktorých čas nemusí byť striktne lineárny.

6. Meranie a pozorovanie:

   • Nelineárne meranie: Ak čas nie je lineárny, môže mať meranie, pri ktorom dochádza ku kolapsu kvantových stavov, iné dôsledky. Pozorovanie by teoreticky mohlo ovplyvniť minulé alebo budúce stavy, čo by viedlo k výpočtom, pri ktorých je časový stav pozorovateľa súčasťou samotného výpočtu.

Súhrnne povedané, nelineárny časový rámec by mohol zásadne zmeniť fungovanie kvantových počítačov a potenciálne rozšíriť ich možnosti nad rámec toho, čo je mysliteľné v lineárnom časovom modeli. Priniesol by však aj jedinečné výzvy, ako napríklad riadenie výpočtov vo viacerých časových stavoch alebo pochopenie správania sa kvantových javov, ako je napríklad kvantové prepojenie, keď časová kauzalita nie je priama. To by si vyžadovalo nielen prehodnotenie kvantových algoritmov, ale možno aj nové definovanie základných pojmov kvantovej mechaniky vo svetle nelineárneho času.

Opísať optimalizačný problém v kontexte nelineárneho času si vyžaduje koncepčný skok z tradičných rámcov riešenia problémov, ale tu je nápaditý príklad:

Plánovanie úloh v časovej závislosti:
Opis: V tomto scenári čas nie je lineárny, ale namiesto toho tvorí komplexnú, vzájomne prepojenú sieť, v ktorej sa minulé, súčasné a budúce udalosti navzájom ovplyvňujú nesekvenčným spôsobom. Tento problém zahŕňa plánovanie úloh pre tím, kde dokončenie jednej úlohy môže ovplyvniť začiatok alebo účinnosť úloh v rôznych „časoch“, nielen tých, ktoré nasledujú chronologicky.

Cieľová funkcia:

• Maximalizovať: Celková produktivita a efektívnosť vo všetkých „časových“ stavoch.

Obmedzenia:

• Každá úloha musí byť dokončená raz vo všetkých časových stavoch.

• Zdroje môžu byť alokované v rôznych časových stavoch, ale nemôžu byť na dvoch miestach súčasne v rámci toho istého časového úseku.

• Úlohy môžu mať závislosti alebo prínosy, ktoré sa vzťahujú na rôzne časové stavy, čo znamená, že dokončenie úlohy v jednom „čase“ by mohlo urýchliť alebo oddialiť úlohy v inom „čase“.

Premenné:

• Priradenie úloh členom tímu a ich umiestnenie v rôznych časových stavoch.

Príklad scenára:

• Uvažujme tím štyroch členov (Alice, Bob, Carol, David), ktorí majú za úlohu dokončiť štyri projekty (P1, P2, P3, P4) v časovej štruktúre, kde

  • P1 v jednom časovom stave (TS1) môže ovplyvniť čas začiatku alebo efektívnosť P2 v inom časovom stave (TS2).

  • Skoré dokončenie P3 v TS3 môže umožniť, aby bol zdroj (napríklad špecializovaný nástroj) k dispozícii skôr v TS1, čo ovplyvní dokončenie P1.

Prístup k riešeniu v nelineárnom čase:

• Reprezentácia na základe grafov: Časové stavy by mohli byť uzlami v grafe, kde hrany predstavujú vplyv alebo závislosť medzi úlohami v čase. Tento graf by nebol lineárny, ale skôr komplexná sieť, kde medzi uzlami existujú slučky alebo viacero ciest.

• Optimalizačný algoritmus:

  • Dynamické programovanie so zvratom: Prispôsobte dynamické programovanie tak, aby sa zohľadnilo nielen to, čo nasleduje, ale aj to, aké vplyvy môžu prichádzať z akéhokoľvek smeru v čase. Vypočítali by ste najlepšiu cestu cez túto časovú sieť, pričom by ste zvážili, ako akcie v jednom stave ovplyvňujú všetky pripojené stavy.

  • Algoritmy inšpirované kvantovou technológiou: Ak si požičiame z konceptov kvantových počítačov, ako sú superpozícia a previazanosť, algoritmus by mohol skúmať viacero scenárov plánovania súčasne, pričom „kolaps“ jedného rozhodnutia o plánovaní by mohol okamžite ovplyvniť rozhodnutia vo všetkých súvisiacich časových stavoch.

• Heuristické alebo evolučné metódy: Použitie genetických algoritmov, kde „chromozóm“ predstavuje rozvrh vo všetkých časových stavoch, pričom mutácie a kríženia umožňujú skúmať, ako zmena časovania jednej úlohy ovplyvňuje celú časovú sieť.

Kľúčové úvahy:

• Spätné slučky: Ako dokončenie úlohy v jednom časovom stave spätne ovplyvňuje jej vlastné nastavenie alebo iné?

• Časová previazanosť: Ak sú úlohy vzájomne previazané, zmena jedného časového plánu si môže okamžite vyžiadať prehodnotenie ostatných bez ohľadu na tradičnú postupnosť.

Tento príklad posúva hranice tradičnej optimalizácie tým, že spochybňuje pojem postupnosti a kauzality, čím zavádza scenár, v ktorom musí optimalizačný proces zohľadňovať holistický vplyv rozhodnutí v nelineárnom časovom rámci. Ide o vysoko teoretické cvičenie, ktoré ilustruje, ako by sa naše chápanie optimalizácie mohlo vyvíjať pri zásadne odlišnom vnímaní času.

Tu je príklad, ako by sa kvantový počítač mohol použiť na riešenie optimalizačného problému, konkrétne so zameraním na kvantový približný optimalizačný algoritmus (QAOA ) na riešenie problému maximálneho rezu:

Problém maximálneho rezu:

Popis: V tomto prípade sa jedná o riešenie problému Max-Cut**, ktorý sa skladá z dvoch častí: 1: Problém Max-Cut sa týka rozdelenia vrcholov grafu na dve množiny tak, aby počet hrán medzi týmito dvoma množinami („rez“) bol maximálny. Je známe, že tento problém je NP-ťažký, čo z neho robí ideálneho kandidáta na kvantové optimalizačné algoritmy.

Cieľová funkcia:

• Maximalizovať: Počet hrán prechádzajúcich medzi dvoma rozdeleniami grafu.

Obmedzenia:

• Každý vrchol musí byť presne v jednom z dvoch oddielov.

Príklad scenára:

• Uvažujme jednoduchý graf s vrcholmi A, B, C, D a hranami spájajúcimi A-B, A-C, B-C, B-D a C-D.

Riešenie pomocou kvantového počítača s využitím QAOA:

1. Kódovanie problému:

   • Každý vrchol grafu je reprezentovaný qubitom. Pre náš graf potrebujeme štyri qubity (jeden pre každý vrchol A, B, C, D).

   • Stav qubitu (0 alebo 1) by určoval, do ktorej oblasti vrchol patrí.

2. Nastavenie kvantového obvodu:

   • Počiatočný stav: Na začiatku sú všetky qubity v superpozícii 0 a 1, čo umožňuje kvantovému počítaču skúmať všetky možné rozdelenia súčasne.

   • Zmiešavací hamiltonián: Týmto sa uplatňujú operácie na pohyb medzi rôznymi konfiguráciami oddielov v kvantovom stavovom priestore.

   • Problémový hamiltonián: Tento je vytvorený tak, aby odrážal cieľ Max-Cut, kde stavy qubitov zodpovedajú priradeniam oddielov a interakcie (entanglement) medzi qubitmi odrážajú hrany grafu. Energia tohto hamiltoniánu je minimalizovaná, keď je rez maximalizovaný.

3. Kroky algoritmu QAOA:

   • Algoritmus zahŕňa postupnosť krokov, v ktorých:

     • Aplikujte miešací hamiltonián s parametrizovanými bránami na preskúmanie rôznych rezov.

     • Aplikujte problémový hamiltonián na posun k stavom, ktoré by maximalizovali rez.

   • Tieto kroky sa opakujú pre niekoľko vrstiev a parametre brán sa optimalizujú pomocou klasického počítača v hybridnom prístupe.

4. Meranie a optimalizácia:

   • Po aplikácii týchto operácií zmerajte qubity. Každý výsledok merania predstavuje jeden možný rez grafu.

   • Meranie sa opakuje mnohokrát, aby sa vybrali vzorky rôznych oddielov.

   • Klasická časť algoritmu potom používa tieto merania na úpravu parametrov kvantového obvodu s cieľom zvýšiť pravdepodobnosť merania stavov, ktoré zodpovedajú dobrým riešeniam.

5. Výsledok:

   • V priebehu iterácií sa kvantový stav v ideálnom prípade vyvíja tak, aby mal vyššiu pravdepodobnosť kolapsu do konfigurácií, ktoré ponúkajú väčšie rezy. Pre náš príklad grafu by optimálne riešenie mohlo rozdeliť vrcholy tak, že A a D budú v jednej množine a B a C v inej, čím sa maximalizuje rez hrán.

Praktické úvahy:

• Hardvérové obmedzenia: Súčasné kvantové počítače sú „zašumené“ a majú obmedzený čas koherencie, takže praktické implementácie často zahŕňajú stratégie na zmiernenie chýb alebo použitie kvantových žíhačov pre špecifické optimalizačné problémy.

• Hybridný prístup: Kvôli týmto obmedzeniam sa často používa hybridný kvantovo-klasický prístup, pri ktorom kvantové počítače vykonávajú ťažkú prácu pri skúmaní priestoru riešení, zatiaľ čo klasické počítače sa starajú o optimalizáciu parametrov a konečné spresnenie riešenia.

Tento príklad demonštruje, ako môžu kvantové počítače využiť kvantovú superpozíciu a kvantové prepojenie na súčasné skúmanie obrovského počtu riešení, čím potenciálne nájdu takmer optimálne alebo optimálne riešenia zložitých optimalizačných problémov, ako je Max-Cut, efektívnejšie ako klasické metódy pre určité prípady. Skutočné zrýchlenie a praktické využitie však závisí od možností kvantového hardvéru a špecifických vlastností problému.

Viac o probléme Max-Cut

Problém Max-Cut je základný problém v teórii grafov a kombinatorickej optimalizácii, ktorý je definovaný takto:

Opis:

• Graf: Dané je, že neorientovaný graf G = (V, E), kde V je množina vrcholov (alebo uzlov) a E je množina hrán spájajúcich tieto vrcholy.

• Rozdelenie: Úlohou je rozdeliť vrcholy na dve disjunktné množiny (často nazývané „strany“ alebo „množiny“) S a T tak, aby V = S ∪ T a S ∩ T = ∅.

Cieľ:

• Cieľ:Maximalizovať rez: Cieľom je nájsť rozdelenie vrcholov, ktoré maximalizuje počet takýchto hrán.

Obmedzenia:

• Každý vrchol musí byť priradený presne k jednej z dvoch množín, S alebo T.

Formálna definícia:

• Matematicky, ak definujeme funkciu x: V → {0, 1}, kde x(v) = 0, ak je vrchol v v množine S a x(v) = 1, ak je v v množine T, cieľom je maximalizovať:

\sum_{(u, v) \v E} \left| x(u) - x(v) \right|

• Tu sa |x(u) - x(v)| rovná 1, ak sú u a v v rôznych množinách (t. j. ak hrana prechádza rezom) a 0 v opačnom prípade.

Príklad:

• Uvažujme jednoduchý graf so štyrmi vrcholmi (A, B, C, D) a piatimi hranami spájajúcimi A-B, A-C, B-C, B-D a C-D. Jedným z možných riešení by mohlo byť umiestnenie A a D do jednej množiny a B a C do druhej, čím by sa odrezali 4 hrany (A-B, A-C, B-D, C-D).

Aplikácie:

• Návrh siete: Napríklad v telekomunikáciách, kde by ste mohli chcieť minimalizovať náklady na prepojenie komponentov znížením počtu prepojení medzi dvoma skupinami.

• Návrh VLSI: Pri rozmiestňovaní obvodov na čipe, kde rezanie menšieho počtu vodičov môže viesť k jednoduchším alebo efektívnejším návrhom.

• Zhlukovanie údajov: Pri zoskupovaní dátových bodov do zhlukov pri maximalizácii rozdielnosti medzi zhlukmi.

Výpočtová zložitosť:

• Max-Cut je známy ako NP-ťažký, čo znamená, že pre veľké grafy nie je nájdenie presného maximálneho rezu v polynomiálnom čase uskutočniteľné so súčasnými klasickými algoritmami, pokiaľ P=NP. To viedlo k vývoju rôznych aproximačných algoritmov a nedávno aj kvantových algoritmov, ako je Quantum Approximate Optimization Algorithm (QAOA), na potenciálne efektívnejšie nájdenie dobrých (ak nie optimálnych) riešení.

Prístupy k riešeniu:

• Presné algoritmy: Pre malé grafy možno použiť hrubú silu alebo dynamické programovanie.

• Heuristika a aproximácia: Pre väčšie grafy sa používajú metódy ako spektrálne rozdelenie, relaxácie semidefinitného programovania alebo lokálne heuristické hľadanie.

• Kvantové výpočty: Algoritmy ako QAOA využívajú kvantovú mechaniku na paralelné skúmanie priestoru riešení s cieľom nájsť vysokokvalitné riešenia za potenciálne kratší čas ako klasické metódy pre špecifické prípady problémov.

Problém Max-Cut tak slúži nielen ako praktická optimalizačná úloha, ale aj ako porovnávacie kritérium výkonnosti rôznych výpočtových prístupov vrátane kvantových výpočtov.

Viac o probléme Max-Cut v kontexte nelineárneho času

Opis problému Max-Cut v kontexte nelineárneho času zahŕňa prehodnotenie spôsobu, akým pristupujeme k riešeniu problému a jeho vnútornej dynamike:

Kontext nelineárneho času:

Opis problému:

• Graf: Zostáva rovnaký, neorientovaný graf G = (V, E).

• Rozdelenie: Cieľom je stále rozdeliť vrcholy do dvoch množín, S a T, ale teraz sa uvažuje o časovej štruktúre, kde kauzalita nie je striktne lineárna.

Cieľ:

• Cieľ: maximalizovať rez: Primárny cieľ sa nemení, stále sa snažíme maximalizovať počet rezov hrán medzi S a T. Spôsob, akým dosiahneme toto riešenie, však môže byť ovplyvnený nelineárnou časovou dynamikou.

Obmedzenia:

• Každý vrchol musí byť presne v jednej množine, ale teraz môžeme uvažovať o tom, ako sa minulé, súčasné a budúce rozhodnutia o umiestnení vrcholov navzájom ovplyvňujú.

Nové úvahy:

• Časová previazanosť: V nelineárnom čase môže rozhodnutie o umiestnení vrcholu do jednej množiny ovplyvniť rozhodnutia prijaté v iných časových stavoch. Napríklad rozhodnutie o umiestnení vrcholu A do množiny S v jednom časovom stave by mohlo ovplyvniť umiestnenie vrcholu B v inom časovom stave, aj keď tradične by sa o B rozhodovalo až po A.

• Slučky spätnej väzby: Ak sa časové slučky vrátia späť alebo sa udalosti navzájom ovplyvňujú v rôznych časových úsekoch, akt prerezania hrany v jednom bode môže spätne alebo preventívne ovplyvniť spôsob rozdelenia iných vrcholov. To by mohlo znamenať, že „najlepšie“ riešenie v jednom časovom stave sa môže posunúť na základe toho, čo sa rozhodlo v inom.

• Viaceré časové riešenia: Namiesto jedného optimálneho riešenia môžu existovať rôzne „optimálne“ rezy v rôznych časových stavoch, pričom najlepšie celkové riešenie zahŕňa skôr dynamické alebo vyvíjajúce sa rozdelenie v čase než statické.

Algoritmický prístup:

• Algoritmy inšpirované kvantovou technológiou: Predstavte si, že používate kvantové algoritmy nielen na paralelné skúmanie riešení, ale aj také, kde qubity predstavujú vrcholy v rôznych „časoch“. Superpozícia qubitov by tu mohla modelovať skúmanie možností rozdelenia na nelineárnej časovej osi, pričom entanglement by predstavoval, ako rozhodnutia v jednom časovom stave ovplyvňujú ostatné.

• Dynamická optimalizácia: Namiesto jednorazového riešenia by ste mohli implementovať dynamický proces, v ktorom sa rozdelenie vyvíja, prípadne optimalizuje v časových slučkách alebo v rôznych „vetvách“ času. Každá iterácia alebo „časový úsek“ by mohol spresniť rozdelenie na základe nových poznatkov z iných časových stavov.

• Nelineárne programovanie: Prispôsobenie optimalizačných techník tak, aby zohľadňovali, ako sa zmeny v jednom časovom stave môžu vlniť a ovplyvniť celú oblasť problému, pričom sa na modelovanie interakcie rozhodnutí v čase používajú koncepty, ako sú nelineárne diferenciálne rovnice alebo časové siete.

Praktický príklad:

• Predstavte si graf, kde každý vrchol predstavuje bod rozhodnutia v časovej osi projektu, ale táto časová os nie je prísne sekvenčná. Rozhodnutie v 4. týždni môže ovplyvniť to, čo sa malo urobiť v 1. týždni, alebo to, čo bude optimálne v 10. týždni. Max-Cut by tu nebol len o maximalizácii rezu hrán v jednom okamihu, ale o optimalizácii v celej tejto sieti vplyvov, kde sú minulé, súčasné a budúce rozhodnutia navzájom prepojené.

Výzvy:

• Konceptualizácia a matematické modelovanie tohto problému by si vyžadovali nové rámce na pochopenie toho, ako sa riešenia vyvíjajú alebo vnímajú v nelineárnom časovom kontexte.

• Pri implementácii by bolo potrebné zohľadniť zložitosť riadenia riešení vo vzájomne prepojenom časovom priestore, kde sa tradičné pojmy príčiny a následku neuplatňujú jednoznačne.

Problém Max-Cut v nelineárnom čase sa v podstate stáva štúdiou toho, ako možno pristupovať k optimalizácii, keď jednosmerné plynutie času nediktuje postupnosť krokov riešenia problému, ale skôr tvorí komplexnú, vzájomne závislú sieť, kde sa riešenia môžu dynamicky vyvíjať alebo dokonca koexistovať vo viacerých časových stavoch.

Ja neviem nič.

---

preklad: Takumi Azadi –>https://tinyurl.com/yxxk3y9a

---

*Entanglement (kvantové prepletenie) je jeden z najzaujímavejších a najdôležitejších javov v kvantovej fyzike, ktorý zohráva kľúčovú úlohu v kvantových počítačoch. Ide o stav, keď sú dve alebo viac kvantových častíc (napríklad qubity) prepojené takým spôsobom, že stav jednej častice je neoddeliteľne spojený so stavom druhej, bez ohľadu na vzdialenosť medzi nimi. To znamená, že ak zmeníte stav jednej častice, okamžite sa zmení aj stav druhej, a to aj keby boli od seba vzdialené napríklad svetelné roky.

Ako funguje entanglement v kvantových počítačoch?

V kvantových počítačoch sa entanglement využíva na spracovanie informácií oveľa efektívnejšie ako v klasických počítačoch. Niekoľko kľúčových vlastností entanglementu:

1. Korelované stavy: Ak máte dva qubity v prepletenom stave, meraním jedného získate informáciu o druhom. Napríklad ak sú prepletené v stave |00⟩ + |11⟩ (tzv. Bellov stav), keď zmeriate prvý qubit a zistíte, že je v stave |0⟩, viete, že druhý qubit bude tiež v stave |0⟩.

2. Paralelizmus: Prepletené qubity umožňujú kvantovým počítačom paralelne spracovať veľké množstvo informácií, čo dramaticky zvyšuje ich výpočtovú silu.

3. Teleportácia informácií: Kvantový entanglement umožňuje tzv. kvantovú teleportáciu, kde sa informácie (kvantový stav) prenesú z jedného miesta na druhé bez fyzického prenosu častice.

4. Kvadrátne zvýšenie možností: Pri nn prepletených qubitoch je možné spracovať až 2n2^n rôznych stavov naraz, čo je exponenciálny nárast oproti klasickým bitom.

Príklad:

Ak máte dva prepletené qubity A a B, ich stav je spoločný, napríklad:

∣ψ⟩=12(∣00⟩+∣11⟩)|\psi⟩ = \frac{1}{\sqrt{2}}(|00⟩ + |11⟩) 

Keď zmeriate qubit A a zistíte, že je v stave |0⟩, automaticky viete, že qubit B je tiež v stave |0⟩, a to okamžite, bez ohľadu na vzdialenosť.

Prečo je entanglement dôležitý?

Entanglement je základným stavebným prvkom kvantových algoritmov, ako sú Shorov algoritmus (na faktorizáciu čísel) alebo Groverov algoritmus (na vyhľadávanie). Bez neho by kvantové počítače nemali takú výraznú výhodu oproti klasickým počítačom.

Entanglement je fascinujúci fenomén, ktorý v sebe nesie náznaky úplne novej formy výpočtovej techniky a pomáha nám pochopiť hlbšie princípy fungovania vesmíru.

ChatGPT

---

**MaxCut je problém z oblasti teórie grafov a kombinatorickej optimalizácie, ktorý je známy tým, že patrí medzi NP-ťažké problémy. To znamená, že efektívny algoritmus na jeho riešenie (v najhoršom prípade) zatiaľ neexistuje. Tento problém je však dôležitý v mnohých praktických aplikáciách, ako sú sietové optimalizácie, strojové učenie alebo kvantové výpočty.

Definícia MaxCut

Cieľom problému MaxCut je rozdeliť vrcholy grafu na dve podmnožiny tak, aby súčet váh hrán medzi týmito podmnožinami bol maximálny.

Formálne:

• Máme neorientovaný graf G=(V,E)G = (V, E), kde VV je množina vrcholov a EE je množina hrán, pričom každá hrana (u,v)∈E(u, v) \in E má váhu w(u,v)w(u, v).

• Úlohou je nájsť také rozdelenie vrcholov VV na dve disjunktné množiny SS a TT (t. j. S∩T=∅S \cap T = \emptyset a S∪T=VS \cup T = V), aby bol súčet váh hrán medzi SS a TT maximálny:

Príklad

Predstavte si graf so 4 vrcholmi V={A,B,C,D}V = \{A, B, C, D\} a hranami s váhami:

• w(A,B)=2w(A, B) = 2,

• w(A,C)=3w(A, C) = 3,

• w(B,D)=4w(B, D) = 4,

• w(C,D)=1w(C, D) = 1.

Ak rozdelíte vrcholy na S={A,D}S = \{A, D\} a T={B,C}T = \{B, C\}, hrany medzi skupinami budú:

• (A,B)(A, B) s váhou 2,

• (A,C)(A, C) s váhou 3,

• (B,D)(B, D) s váhou 4.

Súčet váh bude 2+3+4=92 + 3 + 4 = 9, čo je optimálne riešenie pre tento graf.

Výzvy

1. NP-ťažkosť: MaxCut je NP-ťažký problém, takže pre veľké grafy neexistuje známy algoritmus, ktorý by vždy našiel optimálne riešenie v rozumnom čase.

2. Aproximácia: Existujú aproximatívne algoritmy, ako napríklad Goemans-Williamsonov algoritmus, ktorý používa semidefinitné programovanie a poskytuje garantovanú aproximáciu s faktorom 0,878.

MaxCut v kvantových výpočtoch

MaxCut sa často používa ako testovací problém pre kvantové počítače, konkrétne v algoritmoch ako QAOA (Quantum Approximate Optimization Algorithm). Kvantové počítače sú schopné riešiť MaxCut efektívnejšie pre niektoré konkrétne prípady, čo ich robí sľubnými pre budúce aplikácie.

Aplikácie

• Optimalizácia sietí: Návrh efektívnych tokov v sieťach.

• Analýza sociálnych sietí: Rozdelenie skupín ľudí s rôznymi preferenciami.

• Fyzika: Modelovanie spinových systémov v kvantovej mechanike.

• Strojové učenie: Rozklad dát na základné zhluky.

MaxCut je fascinujúci problém, ktorý ilustruje prepojenie medzi teóriou grafov, výpočtovou zložitosťou a praktickými aplikáciami v modernej technológii.

ChatGPT

---